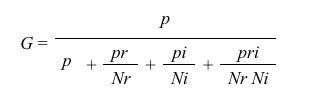このページでは，山西（2005）の資料と同じデータを使用して，
(1) 参加者（被験者），(2) 評定者，(3) 項目（観点）の3つがある場合に，
Rで一般化可能性理論を実行する方法を説明する。
※ Rでは一般化可能性理論のみを扱ったパッケージはない（2012年3月現在）

＜参照した資料＞
自由英作文評価の改善：評定結果の診断的活用（山西博之先生）
Rによる一般化可能性理論の練習（奥村泰之先生）

＜一般化可能性理論の説明で読んでおくべきもの＞
山森光陽 (2004).「英会話テストの信頼性の検討－一般化可能性理論―」
前田啓朗・山森光陽 (編著) 磯田貴道・廣森友人 (著)『英語教師のための
教育データ分析入門：授業が変わるテスト・評価・研究』(pp. 82–91).
大修館

 

---

■ 分析前にやっておくこと

(1) Rのインストール
(2) 作業ディレクトリの確認と変更をしておく
(3) 作業ディレクトリにデータを入れておく
(4) 必要なパッケージをインストールしておく

 

---

■ データの読み込み

説明使用データ（右クリックで「別名で保存」して作業ディレクトリに入れる）

dat <- read.csv("G.csv", header=TRUE, fileEncoding="CP932")
# fileEncoding="CP932"はMacの場合入れる

＜参考＞ 個人データを復元する方法

※ もしくは，Excel を開いてデータ範囲をコピーしてから読み込む
（クリップボードからのデータ読み込み）

Macの場合

dat <- read.table(pipe("pbpaste"), header=TRUE)  
#header=TRUEで変数名を含む，FALSEにすると含まない

Windowsの場合

dat <- read.table("clipboard", header=TRUE) 
#header=TRUEで変数名を含む，FALSEにすると含まない

※ サイトに置いているファイルを直接読み込む場合
（以下をコピーアンドペーストでコンソールに貼付ける）

 dat <- read.csv("http://mizumot.com/handbook/wp-content/uploads/G.csv",header=T, fileEncoding="CP932")

 

■ データの加工

# 変数名の変更
# 元データは生徒，評定者，項目，得点の順なので以下のように変更
colnames(dat) <- c("subj","judge","item","value")

# 得点以外を因子の型に変更
dat$subj <- factor(dat$subj)
dat$judge <- factor(dat$judge)
dat$item <- factor(dat$item)
dat  # 変数名が変更されている事を確認

 

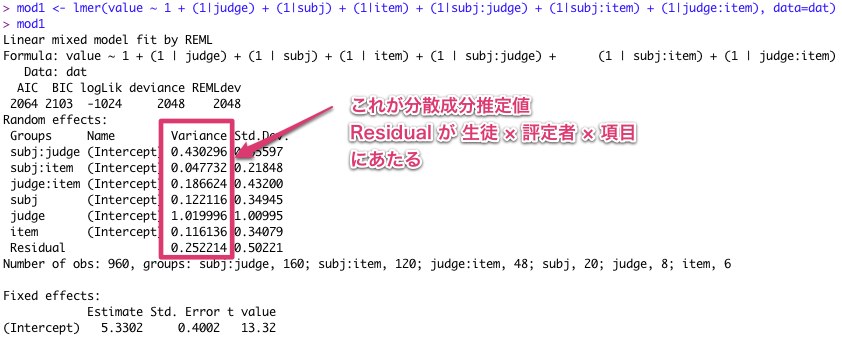
■ 分散成分の推定

library(lme4)  # lme4パッケージ使用
mod1 <- lmer(value ~ 1 + (1|judge) + (1|subj) + (1|item) + (1|subj:judge) + (1|subj:item) + (1|judge:item), data=dat)
mod1

 

■ 分散成分の抽出

varcomp <- VarCorr(mod1)  # VarCorrでrandom effectsの出力を取り出す

output <- rep(NA, length(varcomp)+1)
for(i in 1:length(varcomp)){
output[i] <- varcomp[[i]][,1]
}
names(output) <- c(names(varcomp), "Residual")
output <- sort(output, na.last=T, decreasing=T)
output["Residual"] <- attr(varcomp, "sc")[[1]]^2
round(output,3)  # 分散成分の大きい順に表示される

# 百分率で表示
round(output/sum(output),3)*100

 

■ 一般化可能性係数（G係数）を算出

山西（2005）の説明

分散成分のうち「生徒」を p，「評定者」を r，「項目」を i，「生徒＊評定者」を pr，「生徒＊項目」を pi，「評定者＊項目」を ri，そして「生徒＊評定者＊項目」をpriと読みかえて，必要なものの推定値を下の計算式に代入します。Nrは評定者数，Niは評価項目数です。

# それぞれを上記までの結果から代入
p  <- output[["subj"]]
pr <- output[["subj:judge"]]
pi <- output[["subj:item"]]
pri  <- output[["Residual"]]

reliability <- function(nr, ni){
  denom <- p + pr / nr + pi / ni + pri / (nr * ni)
  G  <- p / denom
  return(G)
}

reliability(nr=8, ni=6)  # 一般化可能性係数（G係数）の算出

# nr は評価者数，ni は項目数なので，値を変更すればシミュレーションが可能
# 以下は，評定者5名，5項目の場合
reliability(nr=5, ni=5)

 

■ 評定者数と項目数の変化によるシミュレーション

# 評定者n名，1-10項目での変化

# --- ここを先に実行 ---
item <- 0:9
ni <- item + 1reliability <- function(nr, ni){
  denom <- p + pr / nr + pi / ni + pri / (nr * ni)
  G  <- p / denom
  return(G)
}
# --- ここまで ---

# nr = 数字 で人数を変えて分析
rater1 <- reliability(nr=1, ni)    # 評定者1名の場合
rater2 <- reliability(nr=2, ni)    # 評定者2名の場合
rater3 <- reliability(nr=3, ni)    # 評定者3名の場合
rater4 <- reliability(nr=4, ni)    # 評定者4名の場合
rater5 <- reliability(nr=5, ni)    # 評定者5名の場合
rater6 <- reliability(nr=6, ni)    # 評定者6名の場合
rater7 <- reliability(nr=7, ni)    # 評定者7名の場合
rater8 <- reliability(nr=8, ni)    # 評定者8名の場合
rater9 <- reliability(nr=9, ni)    # 評定者9名の場合
rater10 <- reliability(nr=10, ni)  # 評定者10名の場合

# 結果
rater1   # 評定者1名の場合
rater2   # 評定者2名の場合
rater3   # 評定者3名の場合
rater4   # 評定者4名の場合
rater5   # 評定者5名の場合
rater6   # 評定者6名の場合
rater7   # 評定者7名の場合
rater8   # 評定者8名の場合
rater9   # 評定者9名の場合
rater10  # 評定者10名の場合

 

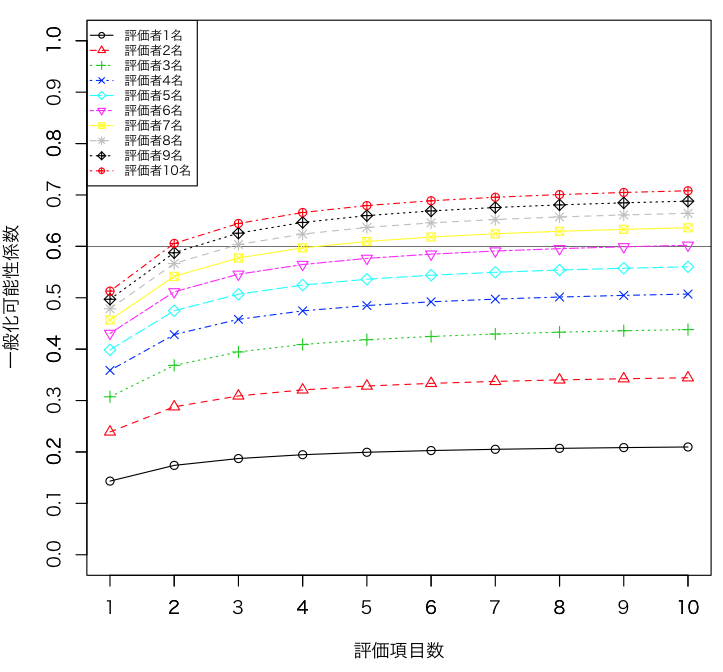
■ シミュレーション結果のグラフ化
（上記までの結果を使ってExcelで描いてもよい）

# 外枠範囲と軸名指定
par(family="HiraKakuPro-W3")  #Macで日本語表記するため
plot(c(0,0),xlim=c(1,10),ylim=c(0, 1),type="n",xlab="評価項目数",ylab="一般化可能性係数")

# 軸の目盛り幅を指定
axis(side=2, at=c(0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1))
axis(side=1, at=1:10)

 # 凡例の追加
legend("topleft", cex=0.7, legend = c("評価者1名","評価者2名","評価者3名","評価者4名","評価者5名","評価者6名","評価者7名","評価者8名","評価者9名","評価者10名"), lty = c(1,2,3,4,5,6,7,8,9,10), pch = c(1,2,3,4,5,6,7,8,9,10), col=c(1,2,3,4,5,6,7,8,9,10))

# y軸の0.6で横線を引いて，実線（lty=1）を0.5の太さ（ltw=0.5）で引く
abline(h=0.6, lwd=0.5, lty=1)

# 評価者数ごとにプロットの点や線の指定（点や線，色は凡例に合わせている）
points(rater1, pch=1, col=1);lines(rater1, col=1, lty=1)
points(rater2, pch=2, col=2);lines(rater2, col=2, lty=2)
points(rater3, pch=3, col=3);lines(rater3, col=3, lty=3)
points(rater4, pch=4, col=4);lines(rater4, col=4, lty=4)
points(rater5, pch=5, col=5);lines(rater5, col=5, lty=5)
points(rater6, pch=6, col=6);lines(rater6, col=6, lty=6)
points(rater7, pch=7, col=7);lines(rater7, col=7, lty=7)
points(rater8, pch=8, col=8);lines(rater8, col=8, lty=8)
points(rater9, pch=9, col=9);lines(rater9, col=9, lty=9)
points(rater10, pch=10, col=10);lines(rater10, col=10, lty=10)