■ 分析前にやっておくこと
(1) Rのインストール
(2) 作業ディレクトリの確認と変更をしておく
(3) 作業ディレクトリにデータを入れておく
(4) 必要なパッケージをインストールしておく
■ 対応のない2群のノンパラメトリック検定(マン・ホイットニーのU検定)
データの読み込み
書籍使用データ(右クリックで「別名で保存」して作業ディレクトリに入れる)
dat <- read.csv("ch08-1MW.csv", header=TRUE, fileEncoding="CP932")
# fileEncoding="CP932"はMacの場合入れる
もしくは,Excel を開いてデータ範囲をコピーしてから読み込む
(クリップボードからのデータ読み込み)
Macの場合
dat <- read.table(pipe("pbpaste"), header=TRUE)
# header=TRUEで変数名を含む,FALSEにすると含まない
Windowsの場合
dat <- read.table("clipboard", header=TRUE)
# header=TRUEで変数名を含む,FALSEにすると含まない
マン・ホイットニーのU検定の実行
result <- wilcox.test(dat$Score~dat$Class, correct=FALSE) # correct=TRUEとしても正確なp値は得られないので使用しないようにする result # z値の計算 pval <- result$p.value z <- qnorm(1-(pval/2)) z # 効果量rの計算 (r = z値/sqrt(サンプル数)で求める) r <- z/sqrt(length(dat$Score)) #lengthはデータ数を確認する関数 r
ここで求められるWはSPSSの結果とは異なるが,結果の W を Mann-Whitney の U
として記載して構わない。説明はこちらを参照。
SPSSの結果と同じ Mann-Whitney の U 検定統計量 を確認したければ,
青木繁伸先生のサイトにあるコードを使用
source("http://aoki2.si.gunma-u.ac.jp/R/src/U_test.R", encoding="euc-jp")
# データをアンスタック形式に変更
x <- data.frame(dat$Score, dat$Class)
y <- unstack(x)
U.test(y$X1, y$X2, correct=FALSE)
■ 対応のある2群のノンパラメトリック検定(ウィルコクソンの符号付順位和検定)
データの読み込み
書籍使用データ(右クリックで「別名で保存」して作業ディレクトリに入れる)
dat <- read.csv("ch08-2wilcoxon.csv", header=TRUE, fileEncoding="CP932")
# fileEncoding="CP932"はMacの場合入れる
attach(dat) #dat$Firstなどと書かなくていいようにattach
※ Excel でデータ範囲をコピーして読み込む方法は,このページの上部を参照。
ウィルコクソンの符号付順位和検定の実行
result <- wilcox.test(First, Second, paired=TRUE, correct=FALSE) result # wilcox.test()についての注意 # z値の計算 pval <- result$p.value z <- qnorm(1-(pval/2)) z # 効果量rの計算 (r = z値/sqrt(サンプル数)で求める) r1 <- z/sqrt(length(dat[,1]*2)) #lengthはデータ数を確認する関数 r1
※Larson-Hall (2010, p. 382)では,効果量rの計算を同順位(タイ)を
カウントせずに純粋なnのみで行っている。その場合は以下の計算。
r2 <- z/sqrt(length(dat[,1])-sum((dat[,2]-dat[,1])==0)) r2
■ 対応のない3群以上のノンパラメトリック検定(クラスカル・ウォリス検定)
データの読み込み
書籍使用データ(右クリックで「別名で保存」して作業ディレクトリに入れる)
dat <- read.csv("ch08-3KW.csv", header=TRUE, fileEncoding="CP932")
# fileEncoding="CP932"はMacの場合入れる
attach(dat) #dat$Firstと書かなくていいようにattach
※ Excel でデータ範囲をコピーして読み込む方法は,このページの上部を参照。
クラスカル・ウォリス検定の実行
result <- kruskal.test(Score~Class) result
※ Field (2005, 2009) や Larson-Hall (2010) は,クラスカル・ウォリス検定では,
効果量の算出が難しく,提示の意味もあまりないことから,多重比較として行う
マン・ホイットニーのU検定のみの効果量を提示すべきであるとしている。
自由度が1ではないカイ2乗値を使って r を算出することに問題があるが,
Morse (2009) や Nye and Hans-Vaughn (2011) では,クラスカル・ウォリス検定で
得られたカイ2乗値を用いて,次の式で η2 (イータ2乗)を求めている。
η2 = カイ2乗値 / (サンプルサイズ-1)
以下はその計算を行った場合。
# 効果量イータ2乗 eta2 <- result$statistic/(length(dat[,1])-1) names(eta2) <- NULL eta2
※ Field (2005, 2009) では,上記のマン・ホイットニーのU検定やウィルコクソンの
符号付順位和検定で行っているように,結果の p 値から,z 値を計算し,それを
r に変換する方法も提案されている。
多重比較
どの組み合わせで差があるのかの多重比較は,マン・ホイットニーのU検定を
組み合わせの数だけ繰り返して行う。p値のみ確認する場合は以下の方法。
# Bonferroniの方法 pairwise.wilcox.test(Score, Class, p.adj="bonferroni", exact=F) # Holmの方法 pairwise.wilcox.test(Score, Class, p.adj="holm", exact=F)
それぞれの組み合わせでマン・ホイットニーのU検定を行う方法。
効果量の計算はこの結果を基に行えばよい(z値とrの計算参照)。
C1.C2 <- subset(dat, Class==1 | Class==2) #1組と2組のみ選択 C1.C3 <- subset(dat, Class==1 | Class==3) #1組と3組のみ選択 C2.C3 <- subset(dat, Class==2 | Class==3) #2組と3組のみ選択 wilcox.test(C1.C2$Score~C1.C2$Class, correct=FALSE) wilcox.test(C1.C3$Score~C1.C3$Class, correct=FALSE) wilcox.test(C2.C3$Score~C2.C3$Class, correct=FALSE)
■ 対応のある3群以上のノンパラメトリック検定(フリードマン検定)
データの読み込み
書籍使用データ(右クリックで「別名で保存」して作業ディレクトリに入れる)
dat <- read.csv("ch08-4Friedman.csv", header=TRUE, fileEncoding="CP932")
# fileEncoding="CP932"はMacの場合入れる
※ Excel でデータ範囲をコピーして読み込む方法は,このページの上部を参照。
フリードマン検定の実行
result <-friedman.test(as.matrix(dat)) # friedman.test()はmatrixしか扱わないので, as.matrixで変換しておく result
※ Field (2005, 2009) や Larson-Hall (2010) は,フリードマン検定では,
効果量の算出が難し難しく,提示の意味もあまりないことから,
多重比較として行うウィルコクソンの符号付順位和検定のみの効果量を
提示すべきであるとしている。
Morse (2009) は,フリードマン検定で得られたカイ2乗値を用いて,
次の式で η2 (イータ2乗)を求めている。
η2 = カイ2乗値 / [サンプルサイズ×(繰り返しの数-1)]
以下はその計算を行った場合。
eta2 <- result$statistic/((length(dat[,1])*(length(dat[1,])-1))) names(eta2) <- NULL eta2
※ Field (2005, 2009) では,上記のマン・ホイットニーのU検定やウィルコクソンの
符号付順位和検定で行っているように,結果の p 値から,z 値を計算し,それを
r に変換する方法も提案されている。
多重比較
どの組み合わせで差があるのかの多重比較は,ウィルコクソンの符号付順位和検定を
組み合わせの数だけ繰り返して行う。p値のみ確認する場合は以下の方法。
#スタック形式に変更 x <- stack(dat) Score <- x[,1] Time <- x[,2] # Bonferroniの方法 pairwise.wilcox.test(Score, Time, p.adj="bonferroni", exact=F, paired=T) # Holmの方法 pairwise.wilcox.test(Score, Time, p.adj="holm", exact=F, paired=T)
それぞれの組み合わせでウィルコクソンの符号付順位和検定を行う方法。
効果量の計算はこの結果を基に行えばよい(z値とrの計算参照)。
wilcox.test(dat$First, dat$Second, paired=TRUE, correct=FALSE) wilcox.test(dat$First, dat$Third, paired=TRUE, correct=FALSE) wilcox.test(dat$Second, dat$Third, paired=TRUE, correct=FALSE)
■ Rcommanderを使う場合
library(Rcmdr) # Rcommanderパッケージの読み込み
コンソールでデータの読み込みができている場合は,
<アクティブデータセットなし>をクリックし,datを選択。
参照 Rコマンダーでデータを読み込む場合
対応のない2群のノンパラメトリック検定(マン・ホイットニーのU検定)
(1) Classを因子の型に変更する。[データ]→[アクティブデータセット内の
変数の管理]→[数値変数を因子に変換]で,「変数」でClassを選択し,
「因子水準」は「数値で」にチェックを入れ,変数の上書きをする。
(2) [統計量]→[ノンパラメトリック検定]→[2標本ウィルコクソン検定]を選び,
OKをクリック。効果量の計算はコンソールを使って行う。
対応のある2群のノンパラメトリック検定(ウィルコクソンの符号付順位和検定)
[統計量]→[ノンパラメトリック検定]→[対応のあるウィルコクソン検定]を選び,
変数を1つずつ選択し,「検定のタイプ」は「正規近似」にチェックを入れて,
OKをクリック。効果量の計算はコンソールを使って行う。
対応のない3群以上のノンパラメトリック検定(クラスカル・ウォリス検定)
(1) Classを因子の型に変更する。[データ]→[アクティブデータセット内の
変数の管理]→[数値変数を因子に変換]で,「変数」でClassを選択し,
「因子水準」は「数値で」にチェックを入れ,変数の上書きをする。
(2) [統計量]→[ノンパラメトリック検定]→[クラスカルーウォリスの検定]を選び,
OKをクリック。効果量の計算や多重比較はコンソールを使って行う。
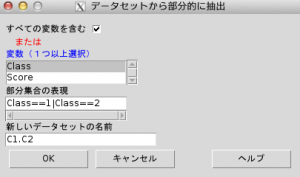
※多重比較は,[データ]→[アクティブデータセット]→[アクティブデータセットの
部分集合を抽出]で, 変数はClassを選び,「部分集合の表現」に
Class==1|Class2 と入力し,クラス1とクラス2のみを選択する。
「新しいデータセットの名前」を入力し,OKをクリックする(下図参照)。
新しいデータセットを使って,クラスカルーウォリスの検定を行うと,
マン・ホイットニーのU検定と同じp値が得られる。
Class2とClass3,Class1とClass3についても同様に多重比較が可能。
対応のある3群以上のノンパラメトリック検定(フリードマン検定)
[統計量]→[ノンパラメトリック検定]→[フリードマンの順位和検定]を選び,
3つ以上の変数を選択し,OKをクリック。
効果量の計算や多重比較を行う必要があればコンソールを使って行う。