t 検定のときの効果量として,r を紹介しています。
平均や標準偏差から計算する効果量の d は,指標として
わかりやすいものですが,t 検定から得られる t 値と自由度(df)を
使って計算する効果量の r は,一体何を示しているのか,
わかりづらいといえば確かにそうだと思います。
大学院の授業でも毎年,学生が混乱しているようですし,
海外のジャーナルに論文を投稿して,査読者から
「この効果量の r という指標は見たことがない」というコメントを
もらったという方もいましたので,説明をここにまとめておきます。
水本・竹内(2008, p. 61)を確認してみるとわかるように,
効果量の r は η (イータ)と同じものです。
ちなみに,t 検定の効果量として説明した r は相関比の
特殊な形であるため,η2 は,分散説明率と呼ばれる
相関係数(r)を 2 乗した r2 やR2 (回帰分析の決定係数,
coefficient of determination)と同じものであると
考えてよい (Field, 2005, p.357)。
そのため,論文には η と書いても構いません。
事実,Hatch and Lazaraton(1991) では,t 検定の効果量は,
r と同じように t 値と自由度で計算していますが,
η として紹介されています。
Hatch, E., & Lazaraton, A. (1991). The research manual: Design and statistics for applied linguistics. Boston: Heinle & Heinle.
効果量の r は η は同じものだと言われても,
なぜ同じなのかわからないと思いますので,
ここでは,外国語教育研究ハンドブック第5章で使われている,
独立した(対応のない)t 検定のデータを使用して確認します。
R をお使いの方は,特別なパッケージは使わずに実行しますので,
コピーアンドペーストして試してみて下さい。
まず,データを読み込んで,t 検定を実行します。
dat <- read.csv(“http://mizumot.com/handbook/wp-content/uploads/ch05independent.csv”, header=T, fileEncoding=”CP932″)
dat # どのようなデータか確認
# 等分散を仮定した t 検定
t.test(dat$Score~dat$Group, var.equal=TRUE)
次に, t 値と自由度から,効果量 r を計算します。
少し長いコードですが,上記の結果から手計算でも
構いませんし,Excelの計算シートを使ってもよいでしょう。
t.result <- t.test(dat$Score~dat$Group, var.equal=TRUE)
r <- sqrt(t.result$statistic[[1]]^2/(t.result$statistic[[1]]^2+t.result$parameter[[1]]))
r
同じデータを使って一元配置の分散分析を行い,
効果量の η2 を計算します。
(t 検定でも分散分析でも得られる p 値は同じになります)
anova(lm(dat$Score~dat$Group))
result <- anova(lm(dat$Score~dat$Group))
eta.squared <- result$”Sum Sq”[1]/(result$”Sum Sq”[1]+result$”Sum Sq”[2])
eta.squared #イータ2乗
上記の結果から得られる η2 はイータを2乗したものなので,
r も同じように2乗して比較してみます。
r^2 # t 値と自由度から計算した効果量 r を2乗したもの
eta.squared #イータ2乗
同じ値になっていることが確認できます。
また,確認のために η2 の2乗を外して r と比較します。
r # t 値と自由度から計算する効果量 r
sqrt(eta.squared) # 2乗を外したイータ
こちらも同じ値になっています。
このように,r は η と同じものであることがわかります。
なぜ違う計算から得られる,r と η が同じ値になるのでしょうか。
t 値と自由度から計算できる,効果量 r は点双列相関係数
(point-biserial correlation coefficient) と同じものです。
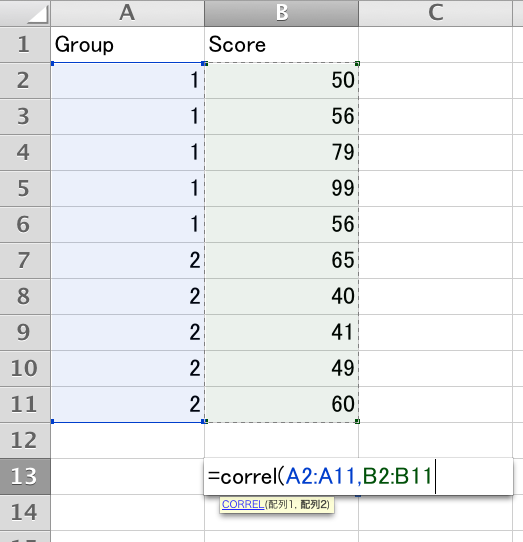
点双列相関とは,以下の図のように,2つのグループを
示す値(1と2)と得点との相関係数のことです。
(グループを示す値は名義尺度なので,1と2でなくても,
2と3だったとしても同じです。)
上記までのデータで,Rを使って計算してみます。
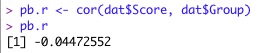
pb.r <- cor(dat$Score, dat$Group)
pb.r
効果量では,正負の符号は関係ありません。
上で計算した,r と η と同じ値になっています。
また,t 値と自由度で計算した効果量rの2乗と,
点双列相関を2乗した値と,分散分析の結果から
計算される η2 の3つを比べてみましょう。
r^2
eta.squared
pb.r^2 #を2乗したもの
同じ値になっていることがわかります。
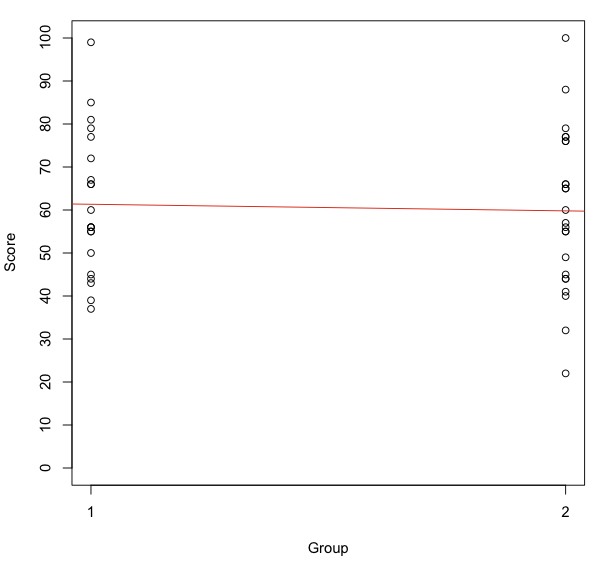
点双列相関をグラフにしてみます。
attach(dat)
plot(Score~Group, ylim=c(0,100), xaxp =c(1, 2, 1), yaxp =c(0, 100, 10))
abline(lm(Score~Group), col=”red”)
グループ1と2の点数に差があれば,回帰直線の傾きも
急になる(つまり,r の値が大きくなる)はずですが,
差がないために,r の値が非常に小さくなっています。
参考までに,r = 0.1(効果量小),r = 0.3(効果量中),
r = 0.5(効果量大)の場合の2つのグループの差を図示します。
(効果量 d も一応入れています)
このように,どちらのグループに振り分けられたかに
よって,点数に差が生じるかどうかというのは,
分散分析における効果量の計算式
η2 = グループ間の平方和 / 平方和の合計
で確認している,「群の効果によるばらつき」
(グループの違いによって生じるばらつき)の割合と
同じものをみているといえるわけです。
結論:効果量の r と η は同じものである。